Source: Wikipedia

Understanding Brewster’s Angle in Optics

Introduction to Brewster’s Angle

Brewster’s angle, named after Sir David Brewster, is a critical concept in optics, particularly when dealing with the reflection and transmission of light between different media. When light hits a boundary between two transparent materials, some of it is typically reflected. However, at a specific angle known as Brewster’s angle, reflection for p-polarized light is minimized.

Polarization and Brewster’s Angle

For light to experience zero reflection at Brewster’s angle, it must be p-polarized. This means that the electric field vector of the light wave oscillates in the plane of incidence. In contrast, s-polarized light, which oscillates perpendicular to the plane of incidence, exhibits higher reflectivity at this angle. As a result, when unpolarized light hits a surface at Brewster’s angle, the reflected light is predominantly s-polarized.

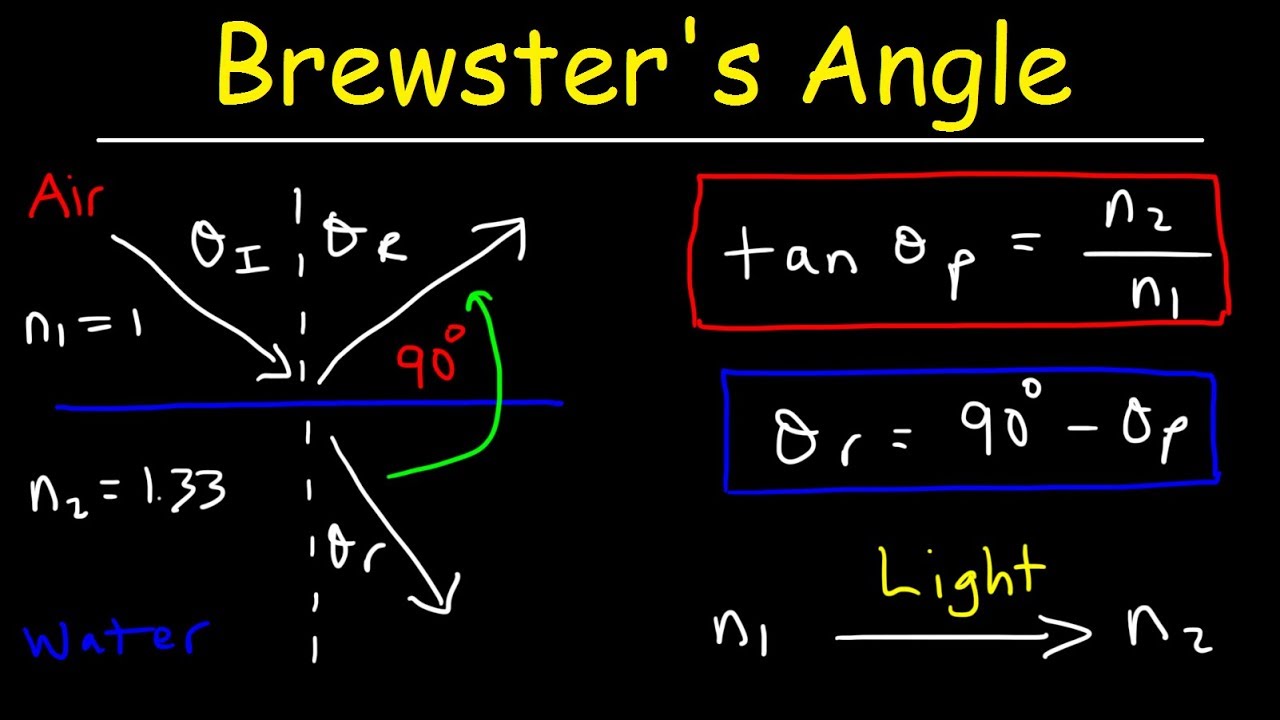
Calculating Brewster’s Angle

The calculation of Brewster’s angle involves the refractive indices of the two media at the boundary. Brewster’s law provides the formula to determine this angle:

Brewster’s angle = arctan(n2/n1)

where n1 and n2 are the refractive indices of the first and second medium, respectively. For example, when light travels from air (n≈1) into glass (n≈1.5), Brewster’s angle is approximately 56.3°.

Applications in Optics

Brewster’s angle finds significant applications in various optical technologies. It is commonly used in laser resonators and other optical setups where minimizing reflection losses is crucial. Optical elements such as laser crystals, birefringent tuners, and prism pairs are often oriented at Brewster’s angle to avoid the need for anti-reflective coatings.

Practical Examples

In laser technology, prisms made of materials like fused silica or SF10 glass are frequently used at Brewster’s angle to achieve low reflection losses. The angle between the prism faces must be chosen carefully to ensure optimal performance. For instance, a fused silica prism with a refractive index of 1.486 at a wavelength of 1064 nm requires an angle of 67.9° for minimal reflection.

Challenges and Considerations

While using Brewster’s angle can reduce reflection losses, it also introduces challenges such as astigmatism in focused beams. This requires additional optical components or design adjustments to mitigate any adverse effects. Additionally, when utilizing Brewster’s angle for attenuating polarized laser beams, care must be taken to manage the s-polarized component, which can dominate the reflected light.

Conclusion

Brewster’s angle is a fundamental concept in optics that offers practical benefits in reducing reflection losses. By understanding and applying this principle, optical engineers can design more efficient systems for a variety of applications, from laser technology to polarizing glasses.

This blog post provides a comprehensive overview of Brewster’s angle, its calculation, applications, and considerations in optics, making it accessible to readers with varying levels of expertise.

Source: YouTube
Feel free to comment your thoughts.