Source: Wikipedia

The Faraday Effect: Understanding Magneto-Optic Phenomena

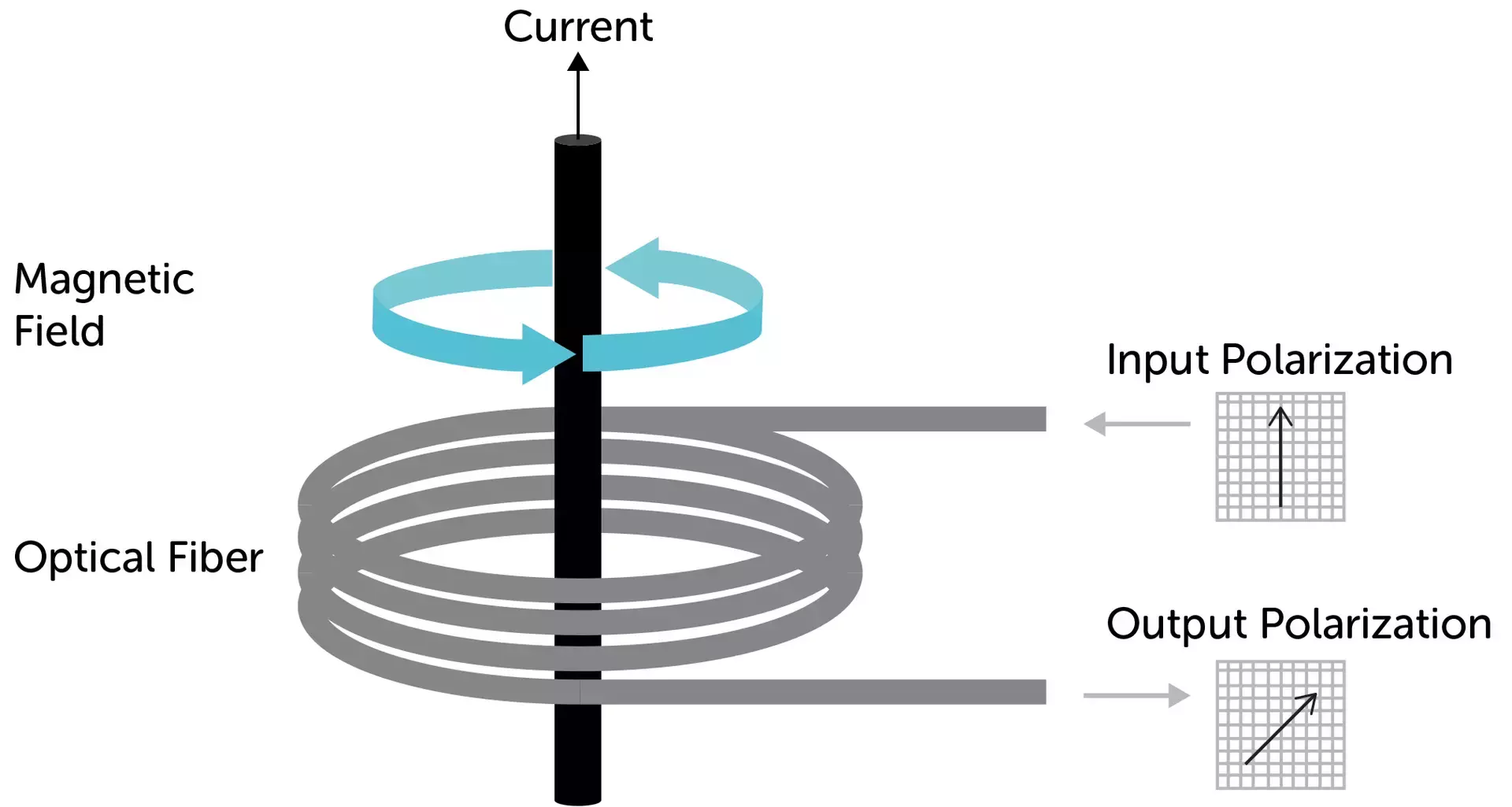
The Faraday Effect, discovered by Michael Faraday in 1845, is a fascinating phenomenon where the polarization direction of light is rotated when it passes through a transparent material in the presence of a magnetic field. This effect has significant implications in the field of photonics and is utilized in various optical devices.

How the Faraday Effect Works

When a linearly polarized light beam travels through a medium exposed to a magnetic field, the polarization direction of the light rotates. The angle of rotation is determined by two factors:

• The Verdet constant of the material, which is a measure of the strength of the effect.
• The magnetic flux density along the direction of light propagation.

The total rotation angle, β, in radians, can be expressed by the formula:

β = V × B × L

Where V is the Verdet constant, B is the magnetic flux density, and L is the length of the material.

Non-reciprocal Nature of the Faraday Effect

A unique aspect of the Faraday Effect is its non-reciprocal nature. This means that if light travels through a Faraday medium and then returns along the same path, the polarization does not revert to its original orientation but instead doubles the rotation. This characteristic is critical for the functioning of devices like optical isolators.

Relation to Circular Birefringence

The rotation caused by the Faraday Effect can be seen as a result of circular birefringence. This is the difference in refractive index between left and right circularly polarized light, as opposed to linear birefringence, which involves orthogonal linear polarization directions.

Verdet Constants and Material Dependence

The Verdet constant varies widely among different materials and wavelengths. Paramagnetic materials generally exhibit higher Verdet constants compared to diamagnetic materials. For instance, Terbium Gallium Garnet (TGG) has a high Verdet constant of −134 rad/(T m) at 623.8 nm, which decreases significantly at longer wavelengths.

The wavelength dependence is partly due to the refractive index difference being proportional to the wavenumber. Additionally, resonance effects in certain materials can enhance the Verdet constant substantially.

Applications of the Faraday Effect

The Faraday Effect is pivotal in the development of various photonics devices:

• Faraday Rotators and Isolators: Used to prevent feedback into laser cavities, ensuring stable laser operation.
• Magneto-Optic Modulators: Though less common, these devices modulate light based on magnetic fields.
• Magnetic Field Sensors: Utilized in fiber-optic sensors for measuring magnetic fields, beneficial in both industrial and astronomical applications.

Conclusion

The Faraday Effect remains a cornerstone of modern photonics, offering insights into light-matter interactions under magnetic influences. Its applications extend from basic research to advanced technological implementations, making it an essential topic of study in the field of optics.

Source: Fibercore – Humanetics
Feel free to comment your thoughts.