Source: YouTube
The Füchtbauer–Ladenburg Equation in Laser Physics
Introduction
The Füchtbauer–Ladenburg equation is a crucial tool in laser physics, particularly in determining the emission cross-sections of laser gain media. This equation helps in understanding the dynamics of fluorescence related to electronic transitions within a medium. By analyzing the fluorescence, scientists can gain insights into the properties of laser materials, which is essential for developing efficient laser systems.
Understanding Fluorescence and Emission Cross-Sections
Fluorescence is the emission of light by a substance that has absorbed light or other electromagnetic radiation. It is a form of luminescence. In laser physics, the fluorescence intensity is directly proportional to the emission cross-section and the cube of the optical frequency. For materials with a narrow emission bandwidth, the frequency factor can be considered constant, simplifying the proportionality to just the emission cross-sections.
Challenges in Measuring Absolute Values
While measuring the spectral shape of fluorescence is relatively straightforward, determining absolute values is more complex. This complexity arises from factors such as doping concentration, electronic excitation levels, collection efficiency, and the photodetector’s responsivity. Due to these variables, absolute scaling often requires alternative methods.
The Role of Quantum Efficiency
The Füchtbauer–Ladenburg method leverages the high quantum efficiency of laser transitions, which implies that the upper-state lifetime is nearly equal to the radiative lifetime. This relationship is quantitatively expressed by the equation:
1/τ_rad = (8πn²/c²) ∫(ν²σ_em(ν) dν) = 8πn²c ∫(σ_em(λ)/λ⁴ dλ)
Here, ν represents the optical frequency, n is the refractive index, c is the speed of light in a vacuum, and σ_em denotes the frequency-dependent emission cross-sections.
Application of the Füchtbauer–Ladenburg Equation
For narrow emission bandwidths, the equation simplifies to:
1/τ_rad ≈ (8πc n²/λ̄⁴) ∫σ_em(λ) dλ
Where λ̄ is the mean wavelength of the transition. This leads to the Füchtbauer–Ladenburg equation:
σ_em(λ) = (λ̄⁴/8πcn²τ_rad) (I(λ)/∫I(λ) dλ)
This formula can be adjusted for broader bandwidths by incorporating wavelength-dependent factors. It is important to note that the fluorescence intensity can be altered when measuring only guided light in optical fibers. For accurate results, spectra should be measured in side light to avoid distortions caused by absorption, amplification, and waveguide effects.
Considerations and Approximations
When using the Füchtbauer–Ladenburg equation, one must consider its limitations and approximations. The equation is most effective for narrow spectra and requires consideration of all lines in a fluorescence spectrum if they span a wide spectral range. Generalizing the equation for broader spectra is possible but requires careful analysis.
Conclusion
The Füchtbauer–Ladenburg equation is an essential component in laser physics, providing insights into the emission properties of laser materials. Understanding the intricacies of this equation allows scientists and engineers to develop more efficient and effective laser systems, enhancing various applications across scientific and industrial fields.
This document provides a comprehensive overview of the Füchtbauer–Ladenburg equation, its application in laser physics, and considerations for its use. It is structured with clear headings and subheadings to guide the reader through the topic.
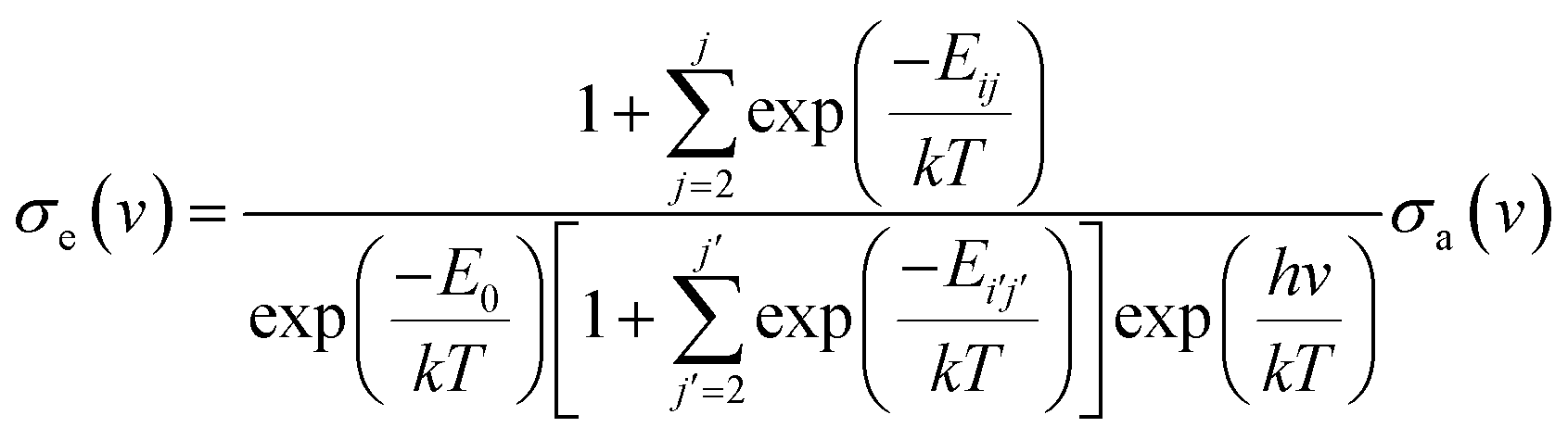
Source: RSC Publishing – The Royal Society of Chemistry
Feel free to comment your thoughts.



