
Source: Optical Tweezers: Principles and Applications
<>
Hermite–Gaussian Modes in Photonics
Introduction
When light propagates in free space or in a homogeneous optical medium, its intensity profile changes. However, Hermite–Gaussian modes are exceptions where the amplitude profile remains constant during propagation.
Understanding Hermite–Gaussian Modes
Hermite–Gaussian modes are approximate solutions of the wave equation for weak focusing. They are characterized by a combination of optical frequency, beam axis, focus position, and beam radius, resulting in a family of modes.
Characteristics of Hermite–Gaussian Modes
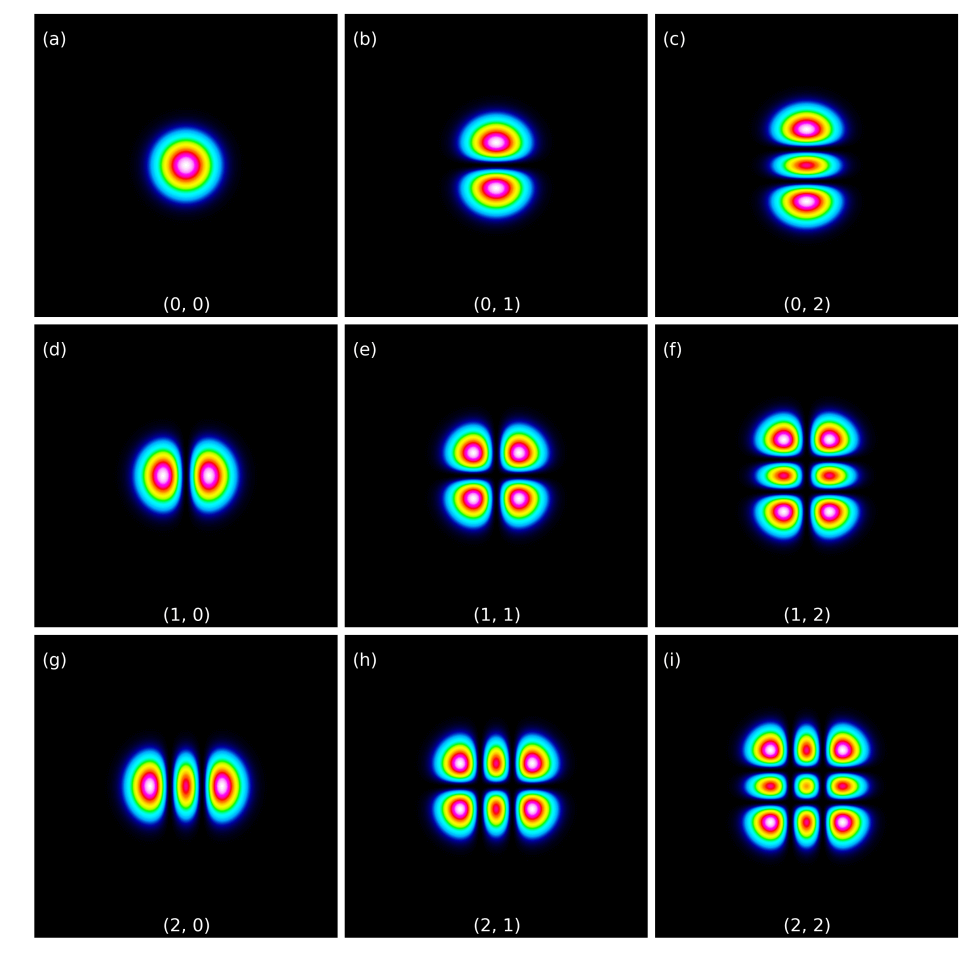
The electric field distributions of Hermite–Gaussian modes are given by the product of a Gaussian function and a Hermite polynomial, with indices determining the shape of the profile in different directions.
Intensity Distribution
The intensity distribution of Hermite–Gaussian modes shows nodes in both horizontal and vertical directions. The fundamental mode, TEM 00, corresponds to a Gaussian beam with the highest beam quality.
Mode Calculations
Software tools like RP Resonator can be used to calculate resonator mode properties for standing-wave and ring resonators, considering factors like alignment sensitivity and thermal lensing.
Applications of Hermite–Gaussian Modes
Hermite–Gaussian modes are commonly used to represent optical resonator modes in laser systems, where they can describe the intensity profile of the output beam.
Excitation of Resonator Modes
A single Hermite–Gaussian resonator mode can be excited by incident laser light if certain conditions are met, such as field overlap and resonance frequency matching.
Comparison with Laguerre–Gaussian Modes
While Laguerre–Gaussian modes are based on polar coordinates and offer rotational symmetry, Hermite–Gaussian modes are preferred in laser systems due to their suitability for non-symmetric components.
Conclusion
Hermite–Gaussian modes play a crucial role in describing the behavior of light in optical systems, particularly in laser resonators, offering a versatile framework for analyzing and understanding beam properties.
Source: DataRay Inc.
Feel free to comment your thoughts.


