Contents
Source: Wikipedia
Understanding Kerr Lens Effect in Optics
When a short optical pulse travels through a nonlinear medium, it experiences the Kerr effect, causing an optical phase delay. This effect is most significant at the beam axis where the optical intensity is highest. The Kerr effect acts like a lens, deforming wavefronts and focusing the pulse. This phenomenon, known as self-focusing, plays a crucial role in passive mode locking of lasers and can also lead to optical damage in media.
Self-Focusing and Self-Defocusing
For a positive nonlinear index, self-focusing occurs, where the pulse is focused due to the Kerr effect. Conversely, for a negative nonlinear index, self-defocusing takes place. This behavior is essential in understanding the behavior of light in nonlinear media.
Kerr Lensing in Gaussian Beams
When a Gaussian beam with optical power and beam radius propagates through a thin piece of a nonlinear medium, a Kerr lens is formed. The dioptric power of this Kerr lens can be calculated using a formula that takes into account the nonlinear index, thickness of the medium, beam radius, and optical power. As the beam focusing becomes stronger, Kerr lensing becomes more prominent, leading to higher optical intensities and intensity gradients.
Applications and Implications
The Kerr lens effect has various applications in optics, such as in mode locking of lasers and studying optical damage in materials. Understanding how the Kerr effect influences the propagation of light in nonlinear media is crucial for designing laser systems and studying nonlinear optical phenomena.
For further exploration of the Kerr lens effect and its applications, additional literature and research in the field of nonlinear optics can provide valuable insights into this fascinating optical phenomenon.
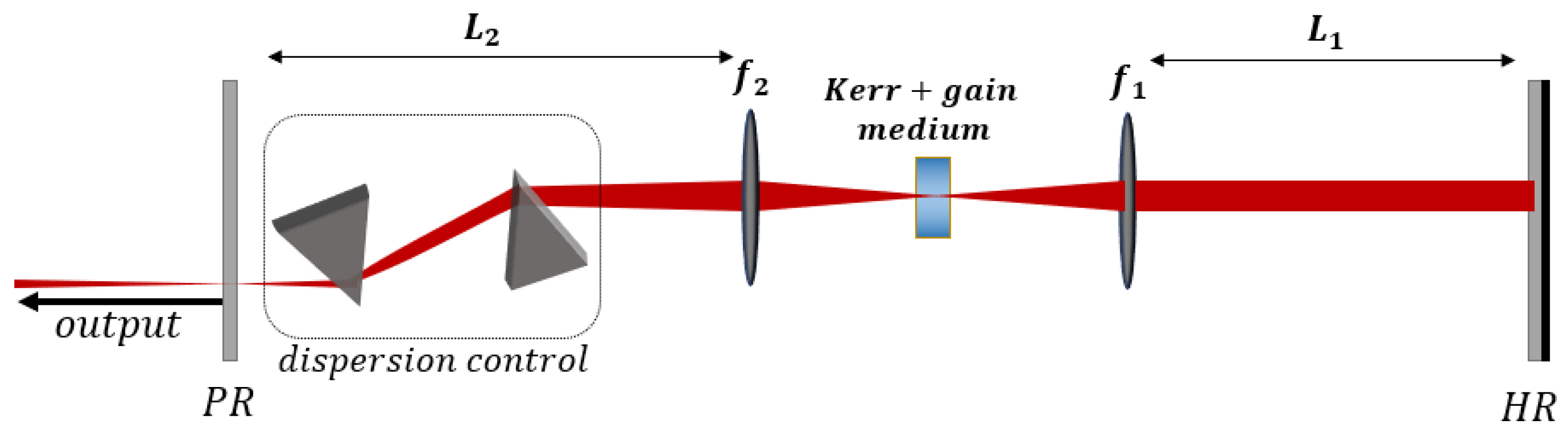
Source: MDPI
Feel free to comment your thoughts.


