Source: SlideServe

Understanding Parametric Nonlinear Interactions

Phase Matching in Nonlinear Interactions

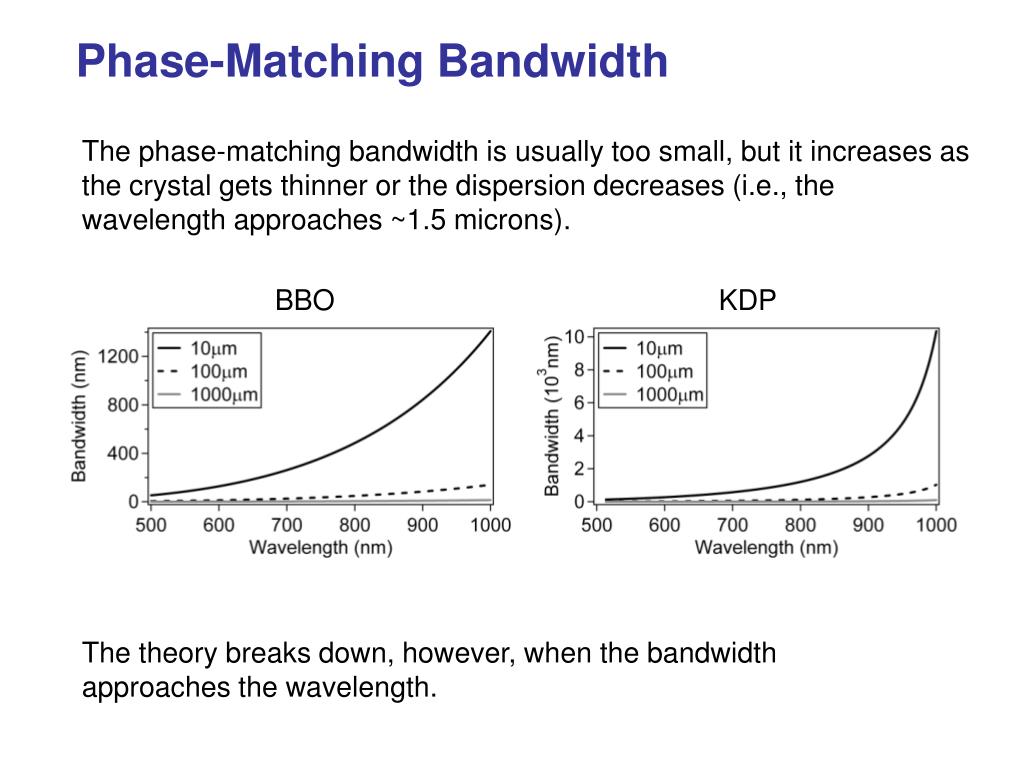
A parametric nonlinear interaction requires phase matching for an efficient exchange of energy. Phase matching ensures a constant phase relationship between interacting waves along the propagation direction. However, due to chromatic dispersion, phase matching is limited to a certain bandwidth, which is influenced by the group velocity mismatch of the waves involved.

Phase Mismatch Calculation

In the context of an optical parametric oscillator with pump, signal, and idler frequencies, the phase mismatch can be calculated as the difference of wavenumbers:

Δk = kp – ks – ki

Phase Matching Bandwidth

The phase-matching bandwidth is defined as the range in which the phase mismatch varies by a certain value (e.g., 2.7831 rad) over the device length. For a crystal of length L, the phase-matching bandwidth can be expressed as:

Δω = 2.7831 / |1/νg,i – 1/νg,s|L

Temporal and Angular Phase Matching

A limited phase-matching bandwidth in the frequency domain corresponds to temporal walk-off in the time domain due to group velocity mismatch. Angular acceptance bandwidth and angular phase-matching bandwidth refer to the range of propagation angles for achieving critical phase matching, which is related to spatial walk-off.

Further Exploration

Understanding phase matching in nonlinear interactions is crucial for various applications in photonics and optics. Exploring the intricacies of phase matching can lead to advancements in areas such as frequency conversion, parametric amplification, and signal processing.

Questions and Comments

If you have any questions or comments regarding phase matching in nonlinear interactions, feel free to share them below.

Source: SlideServe
Feel free to comment your thoughts.