Source: MDPI

Understanding Third-Order Dispersion in Photonics

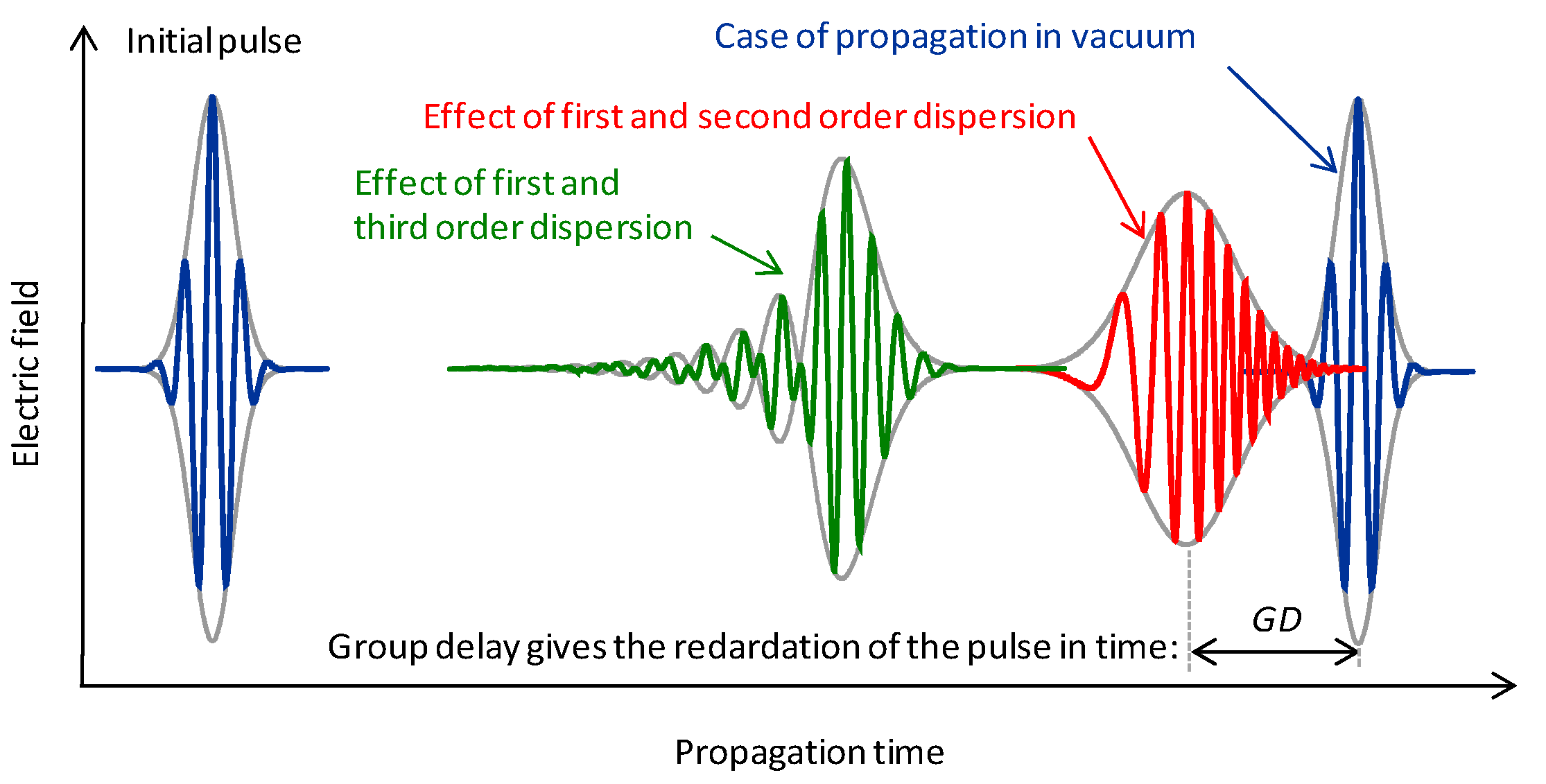
Introduction to Chromatic Dispersion

Chromatic dispersion is a fundamental concept in the field of optics and photonics, describing how different wavelengths of light travel at different speeds through a medium. This phenomenon is crucial in various applications, including fiber optics and laser technology, where precise control over light propagation is essential.

What is Third-Order Dispersion?

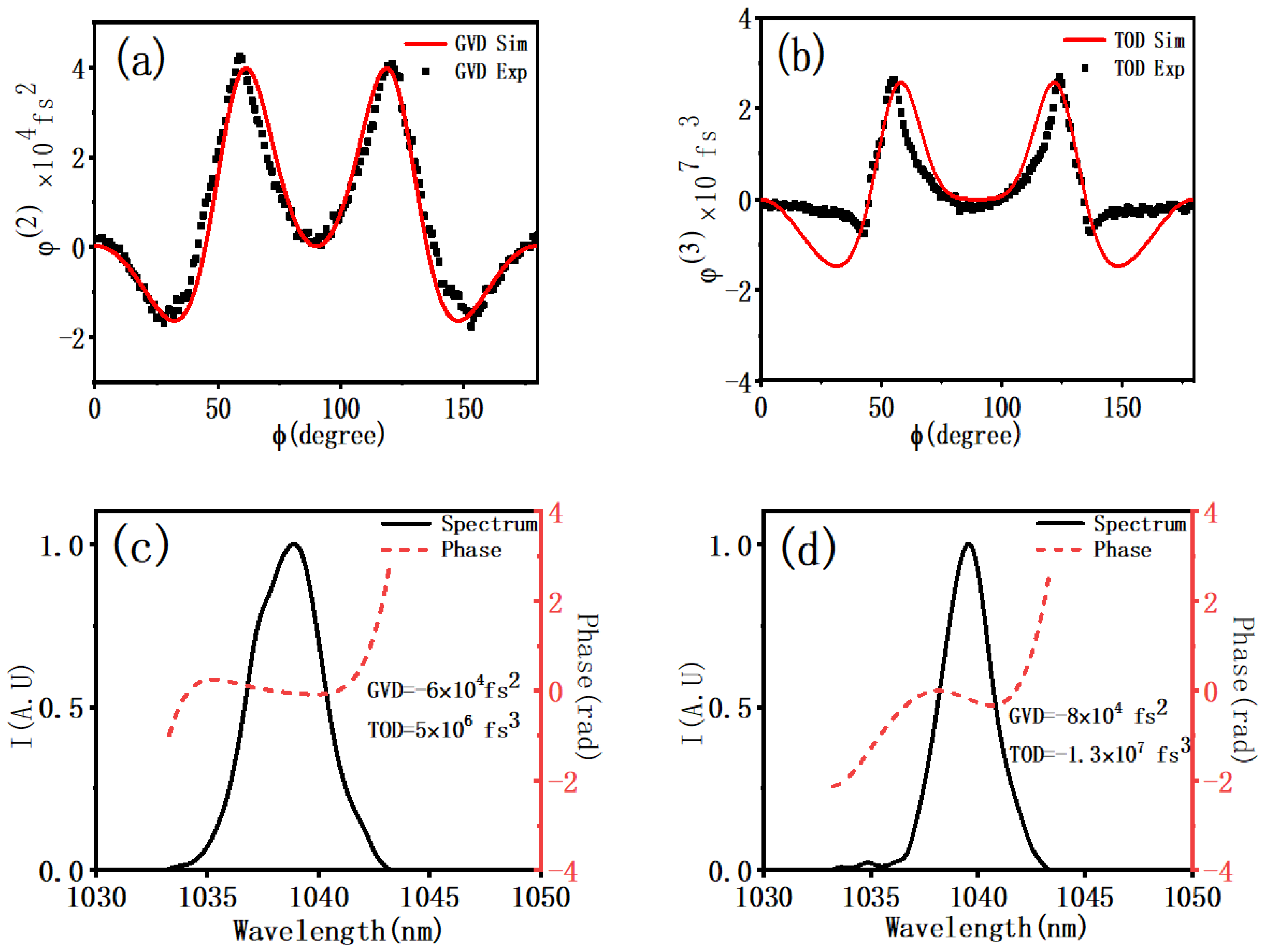
Third-order dispersion (TOD) is an advanced aspect of chromatic dispersion that involves the frequency dependence of group delay dispersion. It is a higher-order effect in the Taylor expansion of spectral phase versus angular frequency offset. Understanding TOD is important for applications requiring high precision, such as ultrafast laser systems.

Mathematical Representation

In mathematical terms, third-order dispersion can be represented as:

k''' = ∂(k'')/∂ω = ∂³φ/∂ω³

Here, k”’ is the third derivative of the wave vector with respect to angular frequency, and it describes the change in group delay per unit length.

Impact on Spectral Phase

The change in spectral phase over a propagation length due to TOD is given by:

Δφ(ω) = (1/6)∂³k/∂ω³ (ω - ω₀)³ L

In this equation, Δφ(ω) represents the change in phase, ω is the angular frequency, ω₀ is the central frequency, and L is the propagation length.

Units and Measurement

TOD is typically measured in units of fs³ (femtoseconds cubed), indicating the degree of dispersion. When specified with respect to vacuum wavelength, the units become fs/nm² (femtoseconds per nanometer squared).

Calculating TOD

The TOD with respect to wavelength can be calculated using the formula:

D₃λ = (2πc/λ²)² ∂³Tg/∂ω² = (2πc/λ²)² ∂³φ/∂ω³

Where D₃λ is the third-order dispersion parameter, c is the speed of light, and λ is the wavelength.

Practical Applications

In mode-locked lasers, particularly those with pulse durations below 30 femtoseconds, compensating for TOD is crucial to maintain pulse integrity. This compensation is necessary alongside second-order dispersion to achieve desired performance.

Numerical Modeling

To analyze the effects of TOD in practical scenarios, numerical pulse propagation modeling is often employed. This approach allows for the simulation of complex interactions within optical systems, providing insights for optimization and design.

Conclusion

Understanding and managing third-order dispersion is essential in advanced photonics applications. By comprehending its mathematical basis and practical implications, researchers and engineers can enhance the performance of optical systems, paving the way for innovations in telecommunications, laser technology, and beyond.

Source: MDPI
Feel free to comment your thoughts.