Source: Wikipedia

<>

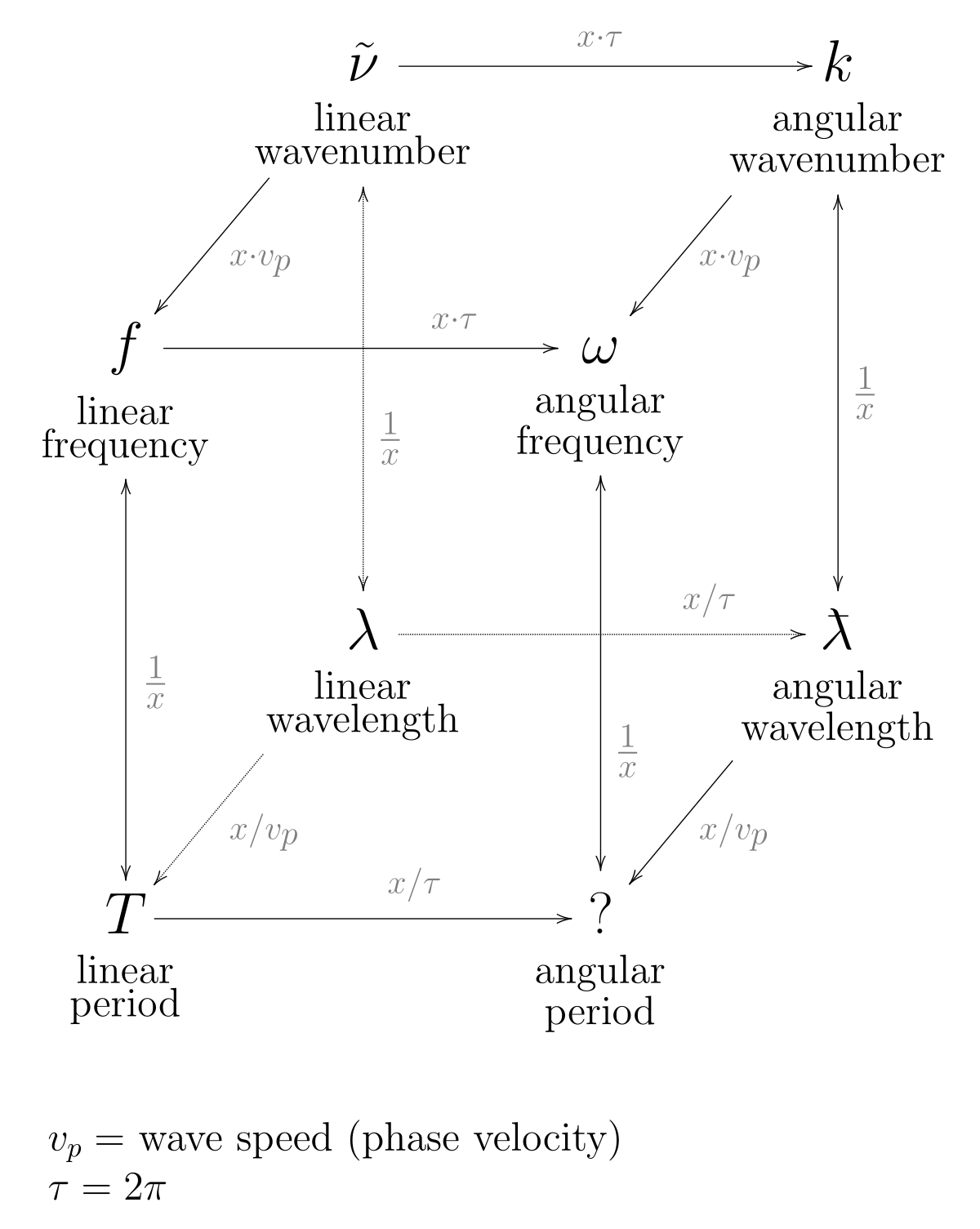
Wavenumber in Physics

In general physics, the wavenumber of light is commonly defined as the magnitude of the wave vector, representing the phase delay per unit length during propagation of a plane wave. For light traveling in a medium, the wavenumber is calculated by multiplying the vacuum wavenumber by the refractive index of the medium. In cases of lossy mediums, the wavenumber can be complex-valued.

The wavenumber is crucial for determining the phase change per unit length of a plane wave in a homogeneous medium. For different types of wave propagation, such as focused beams or guided waves in waveguides, modifications to the phase change per unit length are observed.

Spectroscopic Wavenumbers

Another definition of wavenumber, known as spectroscopic wavenumber, is widely used in spectroscopy. It is based on the wavelength in vacuum and is expressed in units of cm^-1. Unlike angular wavenumbers, spectroscopic wavenumbers are always real values and are preferred in spectroscopic measurements due to standardization issues related to the refractive index of air.

Spectroscopic wavenumbers are commonly utilized for specifying bandwidth or spectral interval width in spectroscopic analyses. For example, a bandwidth of 1 cm^-1 corresponds to a frequency range of approximately 30 GHz.

In practice, wavenumbers are often determined through interferometric measurements rather than direct frequency measurements, making them a practical standard in spectroscopy applications.

Conclusion

Understanding wavenumbers is essential in various fields of physics, particularly in optics and spectroscopy. Whether dealing with angular wavenumbers in general physics or spectroscopic wavenumbers in spectroscopy, these concepts play a crucial role in analyzing and characterizing light waves and their properties.

Source: YouTube
Feel free to comment your thoughts.